베지어 곡선이란 (Bézier Curve)
베지어 곡선(Bézier Curve)은 컴퓨터 그래픽스에서 널리 사용되는 곡선으로, 조절점을 통해 정의됩니다.
이 곡선은 다양한 조절점의 수에 따라 그 형태가 달라지며,
특히 CSS 애니메이션에서 도형을 그릴 때, 백터 그래픽스나 고급 애니메이션을 다룰 때 유용하게 사용됩니다.
이번에는 베지어 곡선의 기본 개념과 카스텔조 알고리즘(De Casteljau’s algorithm)을 포함한 수학적 정의를 살펴보겠습니다.
베지어 곡선이 사용되는 곳

- 웹 애니메이션
- CSS 애니메이션에서 이징 함수로 사용되어 애니메이션의 가속과 감속을 부드럽게 조정합니다.
- 예를 들어, cubic-bezier 함수를 사용하여 custom easing 효과를 만들 수 있습니다.
- SVG
- SVG에서 경로를 그릴 때 사용됩니다.
- 예를 들어 C (큐빅 곡선) 및 Q (퀘드 곡선) 명령어를 통해 복잡한 도형을 생성합니다.
- 로고나 아이콘 디자인에 자주 활용됩니다.
- 타이포그래피
- 글꼴 디자인에서 글자의 곡선을 정의하는 데 사용됩니다.
- 글꼴 제작 소프트웨어(예: FontForge)에서 Bézier 곡선을 이용해 글자의 형태를 조정합니다.
- 게임 개발
- 캐릭터나 오브젝트의 움직임을 부드럽게 만들기 위해 게임 엔진에서 Bézier 곡선을 사용합니다.
- 예를 들어, Unity나 Unreal Engine에서 경로 애니메이션을 구현할 때 활용됩니다.
- 모션 그래픽스
- 비디오 편집 소프트웨어(예: Adobe After Effects)에서 애니메이션의 경로를 설정하거나 효과를 적용하는 데 사용됩니다.
- Bézier 곡선을 통해 부드러운 전환 효과를 생성할 수 있습니다.
- 3D 모델링
- 3D 소프트웨어(예: Blender, Maya)에서 모델의 형태를 정의하는 데 Bézier 곡선이 사용됩니다.
- 복잡한 형상을 만들거나 애니메이션 경로를 설정하는 데 유용합니다.
- 데이터 시각화
- 차트 및 그래프에서 데이터 포인트를 부드럽게 연결하기 위해 Bézier 곡선을 사용하여 정보를 시각적으로 표현합니다.
- 예를 들어, 선형 차트에서 데이터의 흐름을 부드럽게 보여줄 수 있습니다.
- 디자인 도구
- Photoshop, Figma와 같은 디자인 도구에서 Bézier 핸들을 사용하여 곡선을 직관적으로 조작하고 복잡한 형태를 쉽게 만들 수 있습니다.
- 이처럼 Bézier 곡선은 다양한 분야에서 중요한 역할을 하며, 시각적 요소의 품질과 사용자 경험을 향상시키는 데 기여합니다.
조절점
베지어 곡선은 조절점(control point)으로 정의됩니다.
조절점의 개수는 2개, 3개, 4개 이상이 될 수 있으며, 각각의 조절점이 곡선의 형태에 중요한 영향을 미칩니다.
두 개의 조절점: 직선
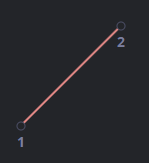
세 개의 조절점: 2차 곡선
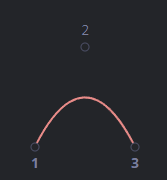
네 개의 조절점: 3차 곡선
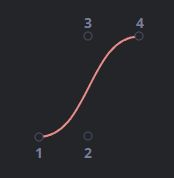
조절점에 대한 베지어 곡선의 특징
조절점과 곡선의 위치
조절점이 곡선 위에 있지 않음
- Bézier 곡선은 조절점을 사용해 정의되지만, 이 조절점들이 곡선 위에 항상 위치하지는 않습니다.
- 예를 들어, 네 개의 조절점이 있을 때 두 조절점 사이에 있는 곡선은 이 조절점들에 의해 영향을 받지만,
곡선 자체는 조절점의 위치에 따라 다르게 형성됩니다.- 이는 곡선이 조절점의 방향과 거리를 기반으로 자연스럽게 만들어지기 때문입니다.
곡선의 차수
곡선의 차수는 조절점의 개수에서 1을 뺀 값으로 정의됩니다.
- 조절점이 2개일 때: 직선 (1차 곡선)
- 조절점이 3개일 때: 2차 곡선 (포물선 형태)
- 조절점이 4개일 때: 3차 곡선 (곡선)
이와 같이 조절점의 개수에 따라 곡선의 형태가 달라지며, 차수가 높아질수록 곡선의 복잡성이 증가합니다.
컨벡스 헐(convex hull)
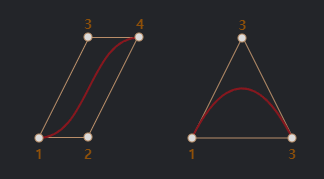
- Bézier 곡선은 항상 조절점의 컨벡스 헐 안에 위치합니다.
- 컨벡스 헐은 조절점을 모두 포함하는 최소의 볼록 다각형을 의미합니다.
- 예를 들어, 조절점들이 삼각형의 꼭짓점에 있다면, 곡선은 그 삼각형의 내부에 위치하게 됩니다.
- 이 특성 덕분에 컴퓨터 그래픽스에서는 교차 검사(intersection test) 최적화가 가능합니다
- 컨벡스 헐은 삼각형, 사각형 같은 상대적으로 단순한 형태입니다
- 따라서 곡선의 교차 여부 보다 컨벡스 헐 교차 여부를 검사하는게 훨씬 쉽습니다
- 따라서 곡선의 컨벡스 헐이 서로 교차하지 않는다면, 곡선 또한 교차하지 않는다는 것을 쉽게 판단할 수 있습니다.
- 컨벡스 헐은 삼각형, 사각형 같은 상대적으로 단순한 형태입니다
조절점 조정
조절점을 움직이면 베지어 곡선은 다시 그려집니다
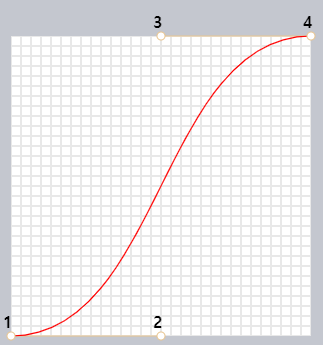
위의 예시를 보면 베지어 곡선이 조절점을 이은 선(1-2, 3-4)을 향해 뻗어나가는 것을 확인 가능합니다
카스텔조 알고리즘
베지어 곡선을 정의하는 공식과 일치하고 곡선이 만들어지는 과정을 시각화 할 때 도움을 주는 알고리즘 입니다
내분을 이용해 곡선을 그리는 알고리즘입니다.
조절점이 3개일 때
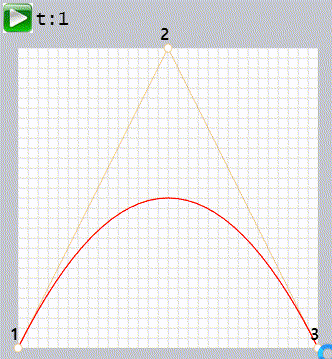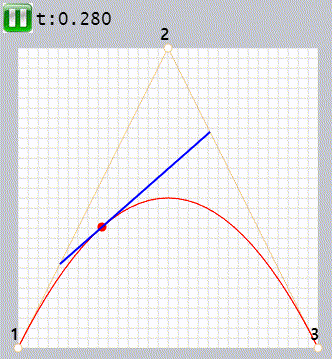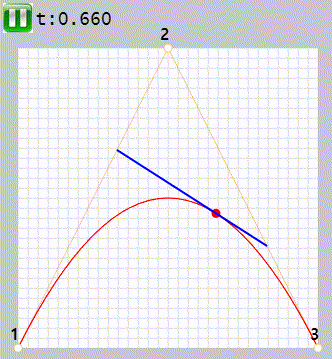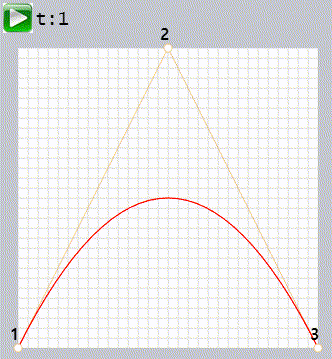
조절점이 3개일 때 베지어 곡선을 만드는 카스텔조 알고리즘은
- 첫번째로,
- 조절점을 찍습니다. 각각 1,2,3으로 이름 붙여두었습니다
- 조절점 1과 2 , 2와 3을 잇는 선분을 만듭니다 (갈색선)
- 매개변수 't'의 값을 0에서 1로 증가 시킵니다
- 't'가 0.05씩 증가해 '0, 0.5, 1, 0.15,... 0.95, 1'이 되도록 하였습니다
- t값으로 추가 작업을 할 수 있습니다
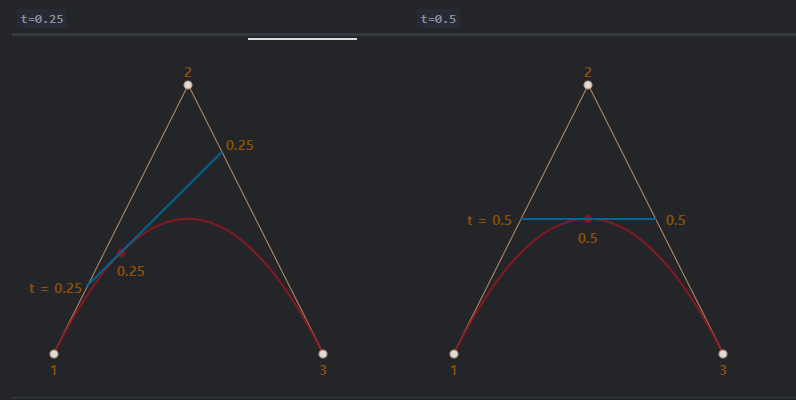
- 갈색으로 표시한 각 선분의 시작점에서 t와 비례하는 위치에 점을 찍는다
- 선분이 두개이므로 점 두개가 만들어집니다
- 두 점을 연결하면 파란선이 만들어집니다.
- 갈색으로 표시한 각 선분의 시작점에서 t와 비례하는 위치에 점을 찍는다
- 파란색 선분에서 t 값과 비례하는 위치에 점 하나를 찍습니다
- t가 0에서 1로 증가하면서 점이 추가 됩니다.
- 이 점들이베지어 곡선을 만듭니다
조절점이 4개일 때
조절점이 4개일 때 베지어 곡선을 만드는 카스텔조 알고리즘은
- 조절점 1과 2, 2와 3, 3과 4를 연결하는 선분을 만듭니다. 총 3개의 갈색 선분이 만들어집니다.
- t를 0부터 시작해 1까지 증가시킵니다
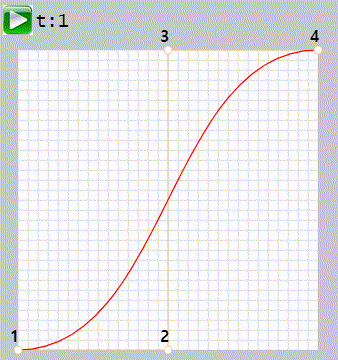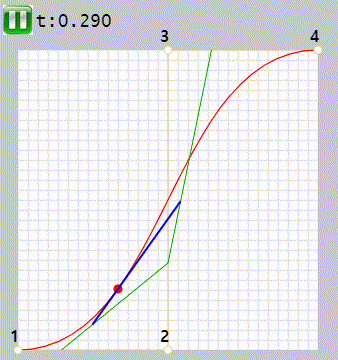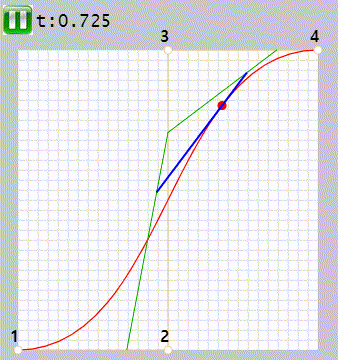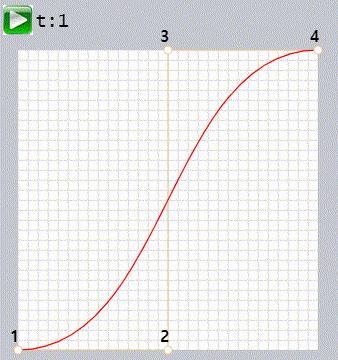
- 선분 시작점에서 t에 비례하는 위치에 점을 찍습니다. 이 점들을 연결해 두 개의 녹색선을 만듭니다.
- 두 개의 녹색 선분 위에 t에 비례하는 위치에 점을 찍습니다. 이 두 점을 연결 파란색 선을 그립니다.
- 파란색 선에서 t에 비례하는 위치에 점(빨간점)을 만듭니다.
- 이 점이 모여 곡선이 만들어집니다.
카스텔조 알고리즘은 재귀적이기 때문에 조절점 개수에 상관없이 일반화가 가능합니다.
N개의 조절점이 있을 때 알고리즘은 다음과 같습니다.
- N개의 조절점을 연결해 N-1개의 선분을 만듭니다.
- 0부터 시작해 1이 될 때까지 t를 조금씩 증가시키면서
각 선분에서 t만큼 비례한 곳에 점을 찍고, 그 선을 연결합니다. 이때 N-2개의 선분이 만들어집니다 - 점이 하나만 남을 때까지 2를 반복합니다.
이렇게 만들어진 점들이 모여 곡선이 됩니다.
카스텔조 알고리즘의 장점
재귀성을 활용한 알고리즘 덕분에 다양한 차수의 베지어 곡선을 쉽게 생성할 수 있습니다.
조절점이 5개, 6개 또는 그 이상의 곡선을 만들 수 있지만, 실제 작업에서는 많은 조절점을 사용하는 경우는 드물습니다.
일반적으로 조절점은 2개에서 3개 정도가 가장 많이 사용되며,
이러한 조절점들을 이용해 만든 곡선을 이어붙여 복잡한 형태를 만들어냅니다.
이 방식을 활용하면 개발과 계산이 훨씬 간단해지는 장점이 있습니다.
이렇게 간단한 구조로 복잡한 그림을 구현할 수 있기 때문에, 실제 애플리케이션에서도 효과적으로 활용되고 있습니다.
베지어 곡선 수학 공식
대다수 공식 없이 마우스로 점을 움직여 원하는 형태의 곡선을 만듭니다
하지만 직접 구현해야하는 경우는 존재하므로 한 번 알아보겠습니다
조절점 Pi의 좌표에 대하여
첫 번째 조절점의 좌표를 P1 = (x1, y1),
두 번째 조절점의 좌표를 P2 = (x2, y2) 등이라 정의했을 때,
베지어 곡선을 이루는 점의 좌표들은 [0,1]사이의 매개변수 t값에 의해 결정됩니다.
1차 베지어 곡선
조절점이 2개일 때 입니다
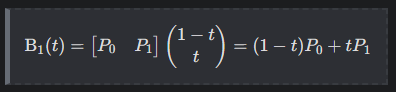
2차 베지어 곡선
조절점이 3개일 때 입니다

3차 베지어 곡선
조절점이 4개일 때 입니다

베지어 곡선 공식 동작 방식
위 식들은 벡터 방정식입니다.
따라서 곡선을 이루는 점의 좌표를 얻을 때 P 대신 x와 y를 넣으면 됩니다.
조절점이 3개인 경우를 예로 들어봅시다. 곡선은 각 점의 좌표 (x,y)를 사용해 만들어집니다.
- x = (1−t)2x1 + 2(1−t)tx2 + t2x3
- y = (1−t)2y1 + 2(1−t)ty2 + t2y3
x1과 y1, x2와 y2, x3과 y3엔 세 조절점의 x, y 좌표를 넣고
t를 0 에서 1로 증가시키면서 도출한 값들을 사용해 곡선을 만듭니다.
조절점이 (0,0), (0.5, 1), (1, 0)인 경우, 방정식은 다음과 같습니다.
- x = (1−t)2 * 0 + 2(1−t)t * 0.5 + t2 * 1 = (1-t)t + t2 = t
- y = (1−t)2 * 0 + 2(1−t)t * 1 + t2 * 0 = 2(1-t)t = –2t2 + 2t
0부터 시작해 1이 될 때까지 t를 증가 시켜 무수히 많은 (x,y) 조합을 만들고, 이를 연결해 곡선을 만들면 됩니다.
'이론 > 프론트엔드' 카테고리의 다른 글
| [Core Web Vitals] 코어 웹 바이탈이란? (2) | 2024.11.29 |
|---|---|
| [알고리즘] JS 자바스크립트 삽입정렬(Insertion Sort), 삽입정렬 알고리즘 코드 (0) | 2024.11.25 |
| [정규표현식] 기본부터 차근차근 알아보기 #11 (정규표현식 \W 문자 약어) (0) | 2024.11.20 |
| [정규표현식] 기본부터 차근차근 알아보기 #10 (정규표현식 \w 문자 약어) (0) | 2024.11.19 |
| [정규표현식] 기본부터 차근차근 알아보기 #9 (복습 - 물음표로 최소한의 횟수로 지정) (0) | 2024.11.18 |
| [정규표현식] 기본부터 차근차근 알아보기 #8 (복습 - 정규표현식 정량자와 중괄호 표기법 비교) (0) | 2024.11.17 |